数学が最初からできなかった訳じゃない。むしろ小学校の算数はそこそこの成績だったんだ。
ところが中学に入ったとたん、急に点数が取れなくなり、二年生になる頃には完全に低迷。以来、数学の姿を見かけるや、コソコソ逃げ回る、まるでジャイアンを見かけた「のび太」のような、私と数学との付き合い。
高校を卒業する時、もう出会うこともない、これからはお互いの道を歩んでいこう、とキッパリ別れを告げたはずの数学が、40年近い歳月を経て、再び私の人生に踏み込んできたのです。
それは、友人の誘いに応じて、学習塾で中学生に英語を教えることになったことが発端でした。
アルバイト講師として、英語の授業は楽しい仕事でした。私自身が体験した「英語を理解していくプロセスの喜び」を、人に伝えることができるからです。
ところが、5科目全教科を対象としている塾であるため、授業時間割の編成上、数学も担当せざるを得なくなったのです。
お前は、数学を誤解している。本当はいい奴なんだ。理解する努力をしてみないか。そんな、天の声だと解釈することにして、中学校時代の古本を引っ張り出すと、そこには奇跡的に、テストの答案用紙が残されていたのです。
時の流れに変色しながらも、答案用紙は「待っていたよ」と微笑んでいるようでした。
「ジャイアン、君ってやつは…」と涙ぐむ「のび太」のごとく、私は答案用紙をめくりながら、45年前の軌跡をたどりました。数学と私との関係が、どこですれ違ってしまったのかを探るために。
答案用紙をめくってほどなく、基本的な計算方法が理解できていないことがわかります。多項式では、÷ の前全体を分子に、後全体を分母にして分数を作るクセがあるのです。÷ が出てきたら逆数にして、乗算でつなげれば良いのに。割り算ができていなかったとは…トホホ。


数学は積み重ねの学問です。つまずいた原因をそのままにして先に進むと、また同じようにつまずきます。つまずいた単元まで立ち返って、勉強をやり直してみることです。
難しく見える問題でも、基本に立ち返って取り組んでみると、理解を深められるだけでなく、もっとシンプルな考え方に気付くこともあります。
これは計算方法に限ったことではありません。中1で習う「比例」の上には中2で習う「1次関数」が、その上には中3で習う「2次関数」が積み重なっています。
広く浅く、という中学校での「理科」や「社会」ならば、新しい単元に入ったら気持ちを切り替え、スタートラインから再出発できます。しかし、縦方向に知識を積み重ねる数学では、1階の工事をきちんとしておかなければ、2階の工事ができません。
かといって数学の世界は、1棟の超高層ビルではありません。数学にも様々な分野があります。いわば複数のビルの集合体です。であれば、ビルの工事や修繕には図面が必要であるように、中学数学にも全体図が必要ではないでしょうか。
「方程式」「関数」「図形」「データ分布」「確率」という名の3階建てビル、その集合が中学数学、と考えれば、今自分がどこにいて、どこに向かうべきか理解できるはずです。
こうした全体図を把握したうえで、私が中学生時代に歯が立たなかった「方程式の利用問題」を、筋道立てて考えてみましょう。
そもそも方程式とは何でしょうか? 「方程式」ビルの1階に行って確認してみましょう。 難しいことを難しいままやろうとせず、簡単に感じるところまで戻って取り組むのです。
「真ん中に=があって,左の式と右の式が等しいことをあらわしたものを『等式』という。『等式』の中でも,未知数(文字)を含んでいるものを『方程式』と呼ぶ。
1種類だけの文字を使った式を『一元方程式』と呼び、その方程式ひとつで,解が限定される。
しかし,文字の種類が2つ以上,つまり,「二元方程式」や「三元方程式」などは,その方程式ひとつでは,解が無数にできてしまうため,方程式を2つ以上組み合わせて解を限定する。」
これが方程式の定理です。これを理解したうえで、ビルの2階に上がり、「連立方程式の利用 (割合) 」の問題にトライしてみましょう。
例として、「8%と3%の食塩水を混ぜ合わせて、6%の食塩水を300g作るとき、2種類の食塩水をそれぞれ何g混ぜればよいか」という問題を考えてみます。
まず、求めるものを文字で表します。この場合、8%の食塩水の量をxg、3%の食塩水の量をygとします。
方程式は「等式」の一つですから、= で表さなければなりません。左辺と右辺が同じ数値のもの、それは、x+y=300 です。
未知数は2つあるので、方程式がもう一つないと、解が限定できません。2種類の食塩水を混ぜ合わせる前と後で、含まれている食塩の量は同じであることに気付けば、8/100 * x +3/100 * y = 300 * 6/100 という等式を作ることができます。
この式を作るためには、「A %とは、A / 100 倍のこと」という、百分率の定理も理解していることが必要です。
あとは連立方程式を解けば、x = 180g , y=120g という解が限定されます。
公式や定理は、解答に必要な「道具」と言えるでしょう。まずは道具を揃えること (公式や定理を理解すること) が必要です。
しかし、道具を揃えることと、道具を使いこなすこととは別物で、数学の難しいところはここにあります。
私は当然の如く「関数」も苦手でした。直線のグラフから座標を読み取る問題では、一生懸命にグラフのマス目を数えたものです。
y=ax+b という、一次関数の式を使うことは思いつきませんでした。これでは、材木をノコギリではなく、金づちでカットしようとするようなものです。
適切な道具を選んだらさらに、足場の悪い場所でも道具を使いこなす技量が必要です。
「三平方の定理」で言えば、直角三角形の形が回転していると、a, b, cのどの部分にどの数字を代入すればいいのか分からなくなってしまう。公式 = 暗記ととらえているので、ちょっと状況が変わっただけで、せっかくの公式や定理が使えなくなってしまうのです。
公式を暗記ではなく、理解すること。三平方の定理ならば、cには一番長い辺(斜辺)が入るなど、公式以外の情報が、問題を解くためには不可欠です。。
教科書によくある形式として「公式の説明→例題→練習問題」というものがあります。その流れで「公式を覚える→その式を使うことがわかっている問題に取り組む」という学習ばかりだと、あらかじめ使う式がはっきりしているため、なぜその式を使うと解けるのか、ということを考える練習にはなりません。
そうした状況のままテストを迎えると、問題を見てもどの公式を用いればよいのか分からず、解答の方針すら立たないという状況に陥りがちです。
覚えるべき公式や定理は限られていても、その使われ方が多岐にわたるため、問題と解き方をセットで丸暗記するような方法を取ろうとすれば、膨大な数のパターンを暗記しなければなりません。
公式や定理といった知識を、適切な状況で引き出し、組み合わせるためには、思考力が強く問われることになります。これが、数学に思考力が必要だといわれるゆえんです。
実際の入試のように「問題を見る→どの知識を使って解くかを考える→実行する」という順で問題に取り組んでみると、使うべき公式や定理に気づくことができるようになるはずです。
数学ができる人には1つ大きな特徴があるといいます。それは問題の対象になっている事柄について、その原理・原則・定義に戻ることができる、ということのようです。数学ができる人は皆、異口同音に「どんな応用問題も基本問題の組み合わせに過ぎない」と言うそうです。
そういう人が、原理・原則・定義に戻って問題を分解している時、解いているだけでワクワクする、夢中になれると言います。そして、解けた時の「あっ!」とひらめいた瞬間、英語でいうところのAha(アハ)体験が、数学の最も面白い部分だそうです。
中学生の私は、「植木算」や「最大公約数」が問題に出ると、花壇を書いたり、数字を片っ端から羅列して条件に合うものを数え上げたりと、公式や定理を利用しようという考えすらありませんでした。ライターがあるのに、木をこすって火を起こそうとするようなものです。
ですから、今こうして振り返ってみて、数学の面白さに出会えなかったことは、ちょっと残念だったなあ、と思います。いや、数学の発想なく生きて来たことは、大きな損失であったかもしれません。
「もっと合理的にできる方法はないだろうか」という、数学的な視点で生活していたら、無為に時間を浪費することはなかったかもしれません。
大工だった父と晩年、一緒に大工工事に行ったことがあります。
写真で見ただけの現場に向かう朝、大工道具が数点入っただけの手提げ袋を持って出かける父を見て、「えっ、これだけ?」と思ったものです。
心配顔の私をよそに、現場では小振りな釘抜きが、材木を仮止めするテコや、時にはハンマーになったりと大活躍。カンナ屑はボンドと混ぜ合わせて、穴埋めのパテに早変わり。
戦時下の学徒動員で、満足に学校にも通えなかった父ですが、シンプルな道具で応用を利かす「数学力」は、相当なものだったのだなあ、としみじみ思います。
それにしても、どうしてこんなにも私は、数学嫌いになってしまったのでしょうか。
十代の反抗心の標的として真っ先に、数学が槍玉に上げられたような気がします。
「♪ 夜の校舎、窓ガラス壊してまわった~」というよりは、「♪ 昼の校舎、窓ガラス拭いてまわった~」というような、いわゆるマジメな生徒だった私は、思春期の反抗心を外に向けることなく、「因数分解なんて、社会に出て何の役に立つ」という主張のもと、勉強を放棄するという、内側への反抗で突っ張ってみたのかもしれません。
遅まきながら、数学の魅力に触れることができて良かったです。
もし人生を、「幸せ = 欲望 / 満足」というシンプルな公式で解釈したなら、もっと生きやすくなるかもしれない。
もし人生の定理を、「人生で飲食できる回数は限られている。ならば、旨い酒を少量いただこう」という考えに定めれば、居酒屋で迷った挙句、オーダーした後も「やっぱり、あっちにすれば良かった」と後悔することも無くなるかな。
この定理は応用もききそう。「人生であと何本の映画を観れるだろう、と考えれば、PCではなく映画館で観よう」とか。
「数学って実生活では、何の役にも立たないじゃないか」と、45年前の私が問うてきたら、今の私はこう答えるでしょう。
「もし、物事を合理的に処理することで、今日より明日をもっと濃密なものにしたいと思うなら、数学の考え方は絶対必要条件だよ」
以下は、中学生時代のテスト結果です。お恥ずかしい。

やはりここでも、分数を割り算にして、わざわざ少数に置き換えています。
方程式の文章問題・関数に対しては、手も足も出ていません。
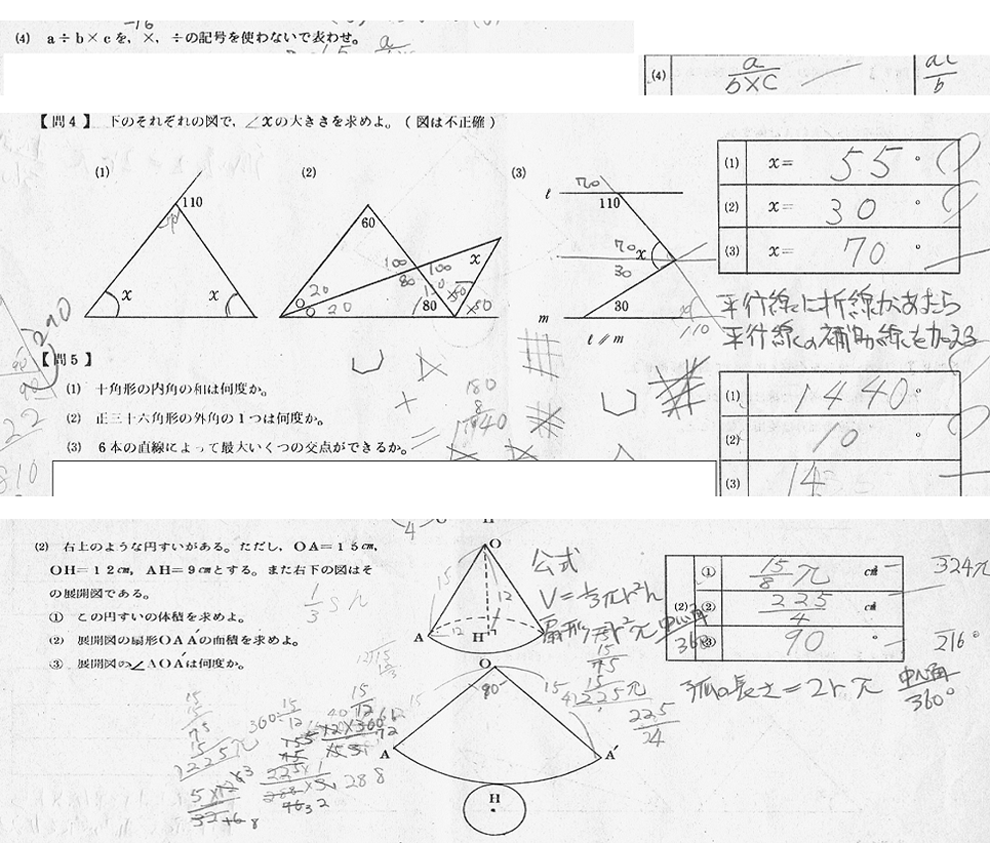
÷ の記号はどうしても鬼門のようです。÷の前後で式を分断してしまうクセが相変わらずです。分数に変化させて乗算で繋いでいくといいのですが。
【問5】(3) 図形問題は公式を使えばすぐ解けるのてすが、公式を知らないので、実際に直線を引いて数えています。あたかも、自分で公式を発見しようとしているかのようです。どの公式を使ったらいいのか、その選択に時間を費やす時間は試験中にありますが、公式を自分で導き出すほどの余裕はありません。
この問題の公式は、直線の数をnとした場合の交点の数「n(n-1)/2」です。漸化式の応用問題であり、現在では中学数学の対象外となっています。

「一次関数は連立方程式を使って解く」という、これまた基本を理解していません。グラフで解こうとして、もがいています。

確率の問題も、「樹形図を書く」という問題解決の方法を知らないようです。

9-(3) 3年生になっても、分数を割り算に置き換えています。

展開でもやはり公式を使わずに、一つ一つ総がけして解いています。
一方で、平方根は得意分野のようです。問題9の二次方程式の問題は、公式による因数分解ではなく、平方根を利用して解こうとしています。惜しくも「2m短い」という設問を逆に解釈してしまったので、正解には至りませんでしたが、発想は間違いではありません。
正解への道筋は一つではないですが、選択肢をたくさん持っているほど、最短距離のルートを選ぶことができます。

三年生になると「三平方の定理」を学びます。定理そのものは、a2 + b2 = c2 を暗記すれば良いのですが、「錐の体積」や「一次関数のグラフ」との組み合わせ問題となっており、中一で学習した「錐の体積と表面積」、中二の「一次関数の式とグラフ」の知識がないと解けません。

7. 植木算の問題は実際に図を書いて正解していますが、最大公約数で全周を割れば答えは出ます。空間状況を数字に置き換える力が、数学の能力といえるでしょう。
10. 確率の問題は、樹形図で考えることが基本です。

一年生から三年生の範囲がまんべんなく出題されています。一次関数のグラフから式を作る方法も、未だに全く理解できていません。こんな状態で、高校入試までに三年間の復習は間に合うのか?
